Sharpe Ratio

A post-hoc test for the Sharpe ratio

Suppose you observe the historical returns of \(p\) different fund managers, and wish to test whether any of them have superior Signal-Noise ratio (SNR) compared to the others. The first test you might perform is the test of pairwise equality of all SNRs. This test relies on the multivariate delta method and central limit theorem, resulting in a chi-square test, as described by Wright et al and outlined in section 4.3 of our Short Sharpe Course. This test is analogous to ANOVA, where one tests different populations for unequal means, assuming equal variance. (The equal Sharpe test, however, deals naturally with the case of paired observations, which is commonly the case in testing asset returns.)

In the analogous procedure, if one rejects the null of equal means in an ANOVA, one can perform pairwise tests for equality. This is called a post hoc test, since it is performed conditional on a rejection in the ANOVA. The basic post hoc test is Tukey's range test, sometimes called 'Honest Significant Differences'. It is natural to ask whether we can extend the same procedure to testing the SNR. Here we will propose such a procedure for a crude model of correlated returns.

The Tukey test has increased power by pooling all populations together to estimate the overall variance. The test statistic then becomes something like

where \(Y_{(1)}\) is the smallest mean observed, and \(Y_{(p)}\) is the largest, and \(S^2\) is the pooled estimate of variance. The difference between the maximal and minimal \(Y\) is why this is called the 'range' test, since this is the range of the observed means.

Switching back to our problem, we should not have to assume that our tested returns series have the same volatility. Moreover, the standard error of the Sharpe ratio is only weakly dependent on the unknown population parameters, so we will not pool variances. In our paper on testing the asset with maximal Sharpe, we established that the vector of Sharpes, for normal returns and when the SNRs are small, is approximately asymptotically normal:

Here \(R\) is the correlation of returns. See our previous blog post for more details. Under the null hypothesis that all SNRs are equal to \(\zeta_0\), we can express this

where \(R^{1/2}\) is a matrix square root of \(R\).

Now assume the simple rank-one model for correlation, where assets are correlated to a single common latent factor, but are otherwise independent:

Under this model of \(R\) we computed inverse-square-root of \(R\) as

Picking two distinct indices, \(i, j\) let \(v = \left(e_i - e_j\right)\) be the contrast vector. We have

because \(v^{\top}1=0\). Thus the range of the observed Sharpe ratios is a scalar multiple of the range of a set of \(p\) independent standard normal variables. This is akin to the 'monotonicity' principle that we abused earlier when performing inference on the asset with maximum Sharpe.

Under normal approximation and the rank-one correlation model, we should then see

with probability \(\alpha\), where the \(q_{1-\alpha,m,n}\) is the upper \(\alpha\)-quantile of the Tukey distribution with \(m\) and \(n\) degrees of freedom. This is computed by qtukey in R. Alternatively one can construct confidence intervals around each \(\hat{\zeta}_i\) of width \(HSD\), whereby if another \(\hat{\zeta}_j\) does not fall within it, the two are said to be Honestly Significantly Different. The familywise error rate should be no more than \(\alpha\).

Testing

Let's test this under the null. We spawn 4 years of correlated returns from 16 managers, then compare the maximum and minimum observed Sharpe ratio, comparing them to the test value of \(HSD\). Assume that the correlation is known to have value \(\rho=0.8\). (More realistically, it would have to be estimated.) Note that for this many fund managers we have

and thus taking into account the \(\sqrt{1-\rho}\) term,

This is only slightly bigger than the naive approximate confidence intervals one would typically apply to the Sharpe ratio, which in this case would be around

We perform 10 thousand simulations, computing the Sharpe over all managers, and collecting the ranges. We compute the empirical type I error rate, and find it to be nearly equal to the nominal value of 0.05:

suppressMessages({
    library(mvtnorm)
})

nman <- 16
nyr  <- 4
ope  <- 252
SNR  <- 0.8   # annual units
rho  <- 0.8

nday <- round(nyr * ope)

R <- pmin(diag(nman) + rho,1)  
mu <- rep(SNR / sqrt(ope),nman)

nsim <- 10000
set.seed(1234)
ranges <- replicate(nsim,{
    X <- mvtnorm::rmvnorm(nday,mean=mu,sigma=R)
    zetahat <- colMeans(X) / apply(X,2,sd)
    max(zetahat) - min(zetahat)
})

alpha <- 0.05
HSDval <- sqrt((1-rho) / nday) * qtukey(alpha,lower.tail=FALSE,nmeans=nman,df=Inf)
mean(ranges > HSDval)

## [1] 0.0541

Compact Letter Display

The results of Tukey's test can be difficult to summarize. You might observe, for example, that managers 1 and 2 have significantly different SNRs, but not have enough evidence to say that 1 and 3 have different SNR, nor 2 and 3. How, then should you think about manager 3? He/She perhaps has the same SNR as 2, and perhaps the same as 1, but you have evidence that 1 and 2 have different SNR. You might label 1 as being among the 'high performers' and 2 among the 'average performers'; In which group should you place 3?

One answer would be to put manager 3 in both groups. This is a solution you might see as the result of compact letter displays, which is a commonly used way of communicating the results of multiple comparison procedures like Tukey's test. The idea is to put managers into multiple groups, each group identified by a letter, such that if two managers are in a common group, the HSD test fails to find they have significantly different SNR. The assignment to groups is actually not unique, and so subject to optimizing certain criteria, like minimizing the total number of groups, and so on, cf. Gramm et al. For our purposes here, we use Piepho's algorithm, which is conveniently provided by the multcompView package in R.

Here we apply the technique to the series of monthly returns of 5 industry factors, as compiled by Ken French, and published in his data library. We have almost 1200 months of data for these 5 returns. The returns are highly positively correlated, and we find that their common correlation is very close to 0.8. For this setup, and measuring the Sharpe in annualized units, the critical value at the 0.05 level is

For comparison, the half-width of the two sided confidence interval on the Sharpe in this case would be

which is a bit bigger. We have actually gained resolving power in our comparison of industries because of the high level of correlation.

Below we compute the observed Sharpe ratios of the five industries, finding them to range from around \(0.49\,\mbox{year}^{-1/2}\) to \(0.67\,\mbox{year}^{-1/2}\). We compute the HSD threshold, then call Piepho's method and print the compact letter display, shown below. In this case we require two groups, 'a' and 'b'. Based on our post hoc test, we assign Healthcare and Other into two different groups, but find no other honest significant differences, and so Consumer, Manufacturing and Technology get lumped into both groups.

# this is just a package of some data:
# if (!require(aqfb.data)) { install.packages('shabbychef/aqfb_data') }
library(aqfb.data)
data(mind5)

mysr <- colMeans(mind5) / apply(mind5,2,FUN=sd)
# sort decreasing for convenience later
mysr <- sort(mysr,decreasing=TRUE)
# annualize it
ope <- 12
mysr <- sqrt(ope) * mysr
# show
print(mysr)

##    Healthcare      Consumer Manufacturing    Technology         Other 
##      0.664421      0.649723      0.602318      0.584746      0.486777

srdiff <- outer(mysr,mysr,FUN='-')
R <- cov2cor(cov(mind5))
# this ends up being around 0.8:
myrho <- median(R[row(R) < col(R)])
alpha <- 0.05
HSD <- sqrt(ope) * sqrt((1-myrho) / nrow(mind5)) * qtukey(alpha,lower.tail=FALSE,nmeans=ncol(mind5),df=Inf)

library(multcompView)
lets <- multcompLetters(abs(srdiff) > HSD)
print(lets)

## $Letters
##    Healthcare      Consumer Manufacturing    Technology         Other 
##           "a"           "a"           "a"           "a"           "a" 
## 
## $LetterMatrix
##                  a
## Healthcare    TRUE
## Consumer      TRUE
## Manufacturing TRUE
## Technology    TRUE
## Other         TRUE

Distribution of Maximal Sharpe, Corrected Bonferroni

In a previous blog post we used the 'Polyhedral Inference' trick of Lee et al. to perform conditional inference on the asset with maximum Sharpe ratio. This is now a short paper on arxiv. I was somewhat disappointed to find, as noted in the paper, that polyhedral inference has lower power than a simple Bonferroni correction against alternatives where many assets have the same Signal-Noise ratio. (Though apparently it has higher power when one asset alone higher SNR.) The interpretation is that when there is no spread in the SNR, Bonferroni correction should have the same power as a single asset test, while conditional inference is sensitive to the conditioning information that you are testing a single asset which has Sharpe ratio perhaps near that of other assets. In the opposite case, Bonferroni suffers from having to 'pay' for a lot of irrelevant (for having low Sharpe) assets, while conditional inference does fine.

I also showed in the paper, as I demonstrated in a previous blog post, that the Bonferroni correction is conservative when asset returns are correlated. In a simple simulations under the null, I showed that the empirical type I rate goes to zero as common correlation \(\rho\) goes to one. In this blog post I will describe a simple trick to correct for average positive correlation.

So let us suppose that we observe returns on \(p\) assets over \(n\) days, and that returns have correlation matrix \(R\). Let \(\hat{\zeta}\) be the vector of Sharpe ratios over this sample. In the paper I show that if returns are normal then the following approximation holds

There is a more general form for Elliptically distributed returns. In the paper I find, via simulations, that for realistic SNRs and large sample sizes, the more general form does not add much accuracy. In fact, for the small SNRs one is likely to see in practice the simple approximation

will suffice.

Now note that, under the null hypothesis that \(\zeta = \zeta_0\), one has

where \(R^{1/2}\) is a matrix square root of \(R\). Testing the null hypothesis should proceed by computing (or estimating) the vector \(z\), then comparing to normality, either by a Chi-square statistic, or performing Bonferroni-corrected normal inference on the largest element.

In the paper I used a simple rank-one model for correlation for simulations using

This effectively models the influence of a common single 'latent' factor. Certainly this is more flexible for modeling real returns than assuming identity correlation, but is not terribly realistic.

Under this model of \(R\) it is simple enough to compute the inverse-square-root of \(R\). Namely

Let's just confirm with code:

p <- 4
rho <- 0.3
R <- (1-rho) * diag(p) + rho
ihR <- (1/sqrt(1-rho)) * diag(p) + (1/p) * ((1/sqrt(1-rho+p*rho)) - (1/sqrt(1-rho))) 
hR <- solve(ihR)
R - hR %*% hR

##             [,1]        [,2]        [,3]        [,4]
## [1,] 4.44089e-16 2.22045e-16 1.11022e-16 1.66533e-16
## [2,] 1.66533e-16 2.22045e-16 5.55112e-17 1.11022e-16
## [3,] 1.11022e-16 1.66533e-16 0.00000e+00 1.11022e-16
## [4,] 1.11022e-16 1.11022e-16 5.55112e-17 1.11022e-16

So to test the null hypothesis, one computes

to test against normality. But note that our linear transformation is monotonic (indeed affine): if \(v_i \ge v_j\) and \(w = \left(R^{1/2}\right)^{-1} v\), then \(w_i \ge w_j\). This means that the maximum element of \(z\) has the same index as the maximum element of \(\hat{\zeta} - \zeta_0\). To perform Bonferroni correction we need only transform the largest element of \(\hat{\zeta} - \zeta_0\), by scaling it up, and shifting to accomodate the average. So if the largest element of \(\hat{\zeta} - \zeta_0\) is \(y\), and the average value is \(a = \frac{1}{p}1^{\top} \left(\hat{\zeta} - \zeta_0\right)\), then the largest value of \(z\) is

Reject the null hypothesis if this is larger than \(\Phi\left(1 - \alpha/p\right)\).

Simulations

Here we perform simple simulations of Bonferroni and corrected Bonferroni. We will assume that returns are Gaussian, that the correlation follows our simple rank one form, that the correlation is known in order to perform the corrected test. We simulate two years of daily data on 100 assets. For each choice of \(\rho\) we perform 10000 simulations under the null of zero SNR, computing the simple and 'improved' Bonferroni corrected hypothesis tests. We tabulate the empirical type I rate and plot against \(\rho\).

suppressMessages({
    library(dplyr)
    library(tidyr)
  library(doFuture)
})
# set up the functions
rawsim <- function(nday,nlatf,nsim=100,rho=0) {
  R <- pmin(diag(nlatf) + rho,1)  
  mu <- rep(0,nlatf)

    apart <- sqrt(nday)/sqrt(1-rho)
    bpart <- sqrt(nday) * ((1/sqrt(1-rho+nlatf*rho)) - (1/sqrt(1-rho)))

  mhtpvals <- replicate(nsim,{
        X <- mvtnorm::rmvnorm(nday,mean=mu,sigma=R)
        x <- colMeans(X) / apply(X,2,sd)
        bonf_pval <- nlatf * SharpeR::psr(max(x),df=nday-1,zeta=0,ope=1,lower.tail=FALSE) 
        # do the correction
        corr_stat <- apart * max(x) + bpart * mean(x)
        corr_pval <- nlatf * pnorm(corr_stat,lower.tail=FALSE)

    c(bonf_pval,corr_pval)
  })
  data_frame(bonf_pvals=as.numeric(mhtpvals[1,]),
                         corr_pvals=as.numeric(mhtpvals[2,]))
}
many_rawsim <- function(nday,nlatf,rho,nsim=1000L,nnodes=7) {
  if ((nsim > 10*nnodes) && require(doFuture)) {
        registerDoFuture()
        plan(multiprocess)
        nper <- as.numeric(table(1:nsim %% nnodes))
    retv <- foreach(iii=1:nnodes,.export = c('nday','nlatf','rho','nper','rawsim')) %dopar% {
            rawsim(nday=nday,nlatf=nlatf,rho=rho,nsim=nper[iii])
    } %>%
      bind_rows()
  } else {
        retv <- rawsim(nday=nday,nlatf=nlatf,rho=rho,nsim=nsim)
  }
  retv
}
mhtsim <- function(alpha=0.05,...) {
  many_rawsim(...) %>%
        tidyr::gather(key=method,value=pvalues) %>%
    group_by(method) %>%
      summarize(rej_rate=mean(pvalues < alpha)) %>%
    ungroup() %>%
    arrange(method)
}

# perform simulations
nsim <- 10000
nday <- 2*252
nlatf <- 100

params <- data_frame(rho=seq(0.01,0.99,length.out=7))

set.seed(123)
resu <- params %>%
  group_by(rho) %>%
    summarize(resu=list(mhtsim(nday=nday,nlatf=nlatf,rho=rho,nsim=nsim))) %>%
  ungroup() %>%
  unnest()

## Error: Problem with `summarise()` column `resu`.
## i `resu = list(mhtsim(nday = nday, nlatf = nlatf, rho = rho, nsim = nsim))`.
## x Interrupted
## i The error occurred in group 1: rho = 0.01.

## Error: Problem with `summarise()` column `resu`.
## i `resu = list(mhtsim(nday = nday, nlatf = nlatf, rho = rho, nsim = nsim))`.
## x Interrupted
## i The error occurred in group 1: rho = 0.01.

suppressMessages({
    library(dplyr)
    library(ggplot2)
})
# plot empirical rates
ph <- resu %>%
    mutate(method=gsub('bonf_pvals','Plain Bonferroni',method)) %>%
    mutate(method=gsub('corr_pvals','Corrected Bonferroni',method)) %>%
  ggplot(aes(rho,rej_rate,color=method)) + 
  geom_line() + geom_point() + 
    geom_hline(yintercept=0.05,linetype=2,alpha=0.5) +
    scale_y_sqrt() + 
    labs(title='Empirical type I rate at the 0.05 level',
             x=expression(rho),y='type I rate',
             color='test')

## Error in mutate(., method = gsub("bonf_pvals", "Plain Bonferroni", method)): object 'resu' not found

print(ph)

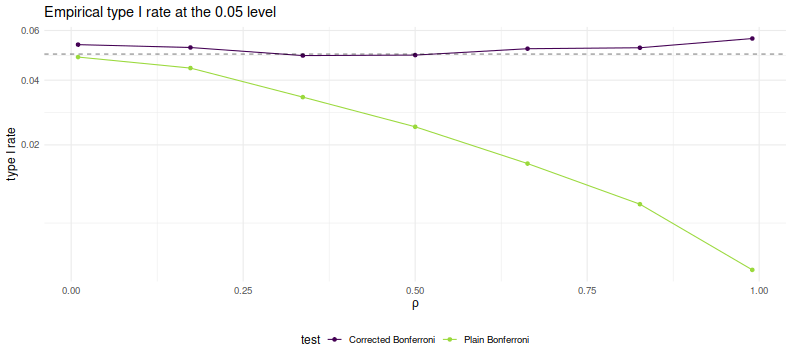
As desired, we maintain nominal coverage using the correction for \(\rho\), while the naive Bonferroni is too conservative for large \(\rho\). This is not yet a practical test, but could be used for rough estimation by plugging in the average sample correlation (or just SWAG'ing one). To my tastes a more interesting question is whether one can generalize this process to a rank \(k\) approximation of \(R\) while keeping the monotonicity property. (I have my doubts this is possible)

Distribution of Maximal Sharpe, Truncated Normal

In a previous blog post we looked at a symmetric confidence intervals on the Signal-Noise ratio. That study was motivated by the "opportunistic strategy", wherein one observes the historical returns of an asset to determine whether to hold it long or short. Then, conditional on the sign of the trade, we were able to construct proper confidence intervals on the Signal-Noise ratio of the opportunistic strategy's returns.

I had hoped that one could generalize from the single asset opportunistic strategy to the case of \(p\) assets, where one constructs the Markowitz portfolio based on observed returns. I have not had much luck finding that generalization. However, we can generalize the opportunistic strategy in a different way to what I call the "Winner Take All" strategy. Here one observes the historical returns of \(p\) different assets, then chooses the one with the highest observed Sharpe ratio to hold long. (Let us hold off on an Opportunistic Winner Take All.)

Observe, however, this is just the problem of inferring the Signal Noise ratio (SNR) of the asset with the maximal Sharpe. We previously approached that problem using a Markowitz approximation, finding it somewhat lacking. That Markowitz approximation was an attempt to correct some deficiencies with what is apparently the state of the art in the field, Marcos Lopez de Prado's (now AQR's?) "Most Important Plot in All of Finance", which is a thin layer of Multiple Hypothesis Testing correction over the usual distribution of the Sharpe ratio. In a previous blog post, we found that Lopez de Prado's method would have lower than nominal type I rates as it ignored correlation of assets.

Moreover, a simple MHT correction will not, I think, deal very well with the case where there are great differences in the Signal Noise ratios of the assets. The 'stinker' assets with low SNR will simply spoil our inference, unlikely to have much influence on which asset shows the highest Sharpe ratio, and only causing us to increase our significance threshold.

With my superior googling skills I recently discovered a 2013 paper by Lee et al, titled Exact Post-Selection Inference, with Application to the Lasso. While aimed at the Lasso, this paper includes a procedure that essentially solves our problem, giving hypothesis tests or confidence intervals with nominal coverage on the asset with maximal Sharpe among a set of possibly correlated assets.

The Lee et al paper assumes one observes \(p\)-vector

Then conditional on \(y\) falling in some polyhedron, \(Ay \le b\), we wish to perform inference on \(\nu^{\top}y\). In our case the polyhedron will be the union of all polyhedra with the same maximal element of \(y\) as we observed. That is, assume that we have reordered the elements of \(y\) such that \(y_1\) is the largest element. Then \(A\) will be a column of negative ones, cbinded to the \(p-1\) identity matrix, and \(b\) will be a \(p-1\) vector of zeros. The test is defined on \(\nu=e_1\) the vector with a single one in the first element and zero otherwise.

Their method works by decomposing the condition \(Ay \le b\) into a condition on \(\nu^{\top}y\) and a condition on some \(z\) which is normal but independent of \(\nu^{\top}y\). You can think of this as kind of inverting the transform by \(A\). After this transform, the value of \(\nu^{\top}y\) is restricted to a line segment, so we need only perform inference on a truncated normal.

The code to implement this is fairly straightforward, and given below. The procedure to compute the quantile function, which we will need to compute confidence intervals, is a bit trickier, due to numerical issues. We give a hacky version below.

# Lee et. al eqn (5.8)
F_fnc <- function(x,a,b,mu=0,sigmasq=1) {
  sigma <- sqrt(sigmasq)
  phis <- pnorm((c(x,a,b)-mu)/sigma)
  (phis[1] - phis[2]) / (phis[3] - phis[2])
}
# Lee eqns (5.4), (5.5), (5.6)
Vfuncs <- function(z,A,b,ccc) {
  Az <- A %*% z
  Ac <- A %*% ccc
  bres <- b - Az
  brat <- bres
  brat[Ac!=0] <- brat[Ac!=0] / Ac[Ac!=0]
  Vminus <- max(brat[Ac < 0])
  Vplus  <- min(brat[Ac > 0])
  Vzero  <- min(bres[Ac == 0])
  list(Vminus=Vminus,Vplus=Vplus,Vzero=Vzero)
}
# Lee et. al eqn (5.9)
ptn <- function(y,A,b,nu,mu,Sigma,numu=as.numeric(t(nu) %*% mu)) {
  Signu <- Sigma %*% nu
  nuSnu <- as.numeric(t(nu) %*% Signu)
  ccc <- Signu / nuSnu  # eqn (5.3)
  nuy <- as.numeric(t(nu) %*% y)
  zzz <- y - ccc * nuy  # eqn (5.2)
  Vfs <- Vfuncs(zzz,A,b,ccc)
  F_fnc(x=nuy,a=Vfs$Vminus,b=Vfs$Vplus,mu=numu,sigmasq=nuSnu)
}
# invert the ptn function to find nu'mu at a given pval.
citn <- function(p,y,A,b,nu,Sigma) { 
  Signu <- Sigma %*% nu
  nuSnu <- as.numeric(t(nu) %*% Signu)
  ccc <- Signu / nuSnu  # eqn (5.3)
  nuy <- as.numeric(t(nu) %*% y)
  zzz <- y - ccc * nuy  # eqn (5.2)
  Vfs <- Vfuncs(zzz,A,b,ccc)

  # you want this, but there are numerical issues: 
  #f <- function(numu) { F_fnc(x=nuy,a=Vfs$Vminus,b=Vfs$Vplus,mu=numu,sigmasq=nuSnu) - p } 
  sigma <- sqrt(nuSnu)
  f <- function(numu) { 
    phis <- pnorm((c(nuy,Vfs$Vminus,Vfs$Vplus)-numu)/sigma)
    #(phis[1] - phis[2]) - p * (phis[3] - phis[2])
    phis[1] - (1-p) * phis[2] - p * phis[3]
  }
  # this fails sometimes, so find a better interval
  intvl <- c(-1,1)  # a hack.
  # this is very unfortunate
    trypnts <- seq(from=min(y),to=max(y),length.out=31)
    ys <- sapply(trypnts,f)
    dsy <- diff(sign(ys))
    if (any(dsy < 0)) {
      widx <- which(dsy < 0)
      intvl <- trypnts[widx + c(0,1)]
    } else {
      maby <- 2 * (0.1 + max(abs(y)))
      trypnts <- seq(from=-maby,to=maby,length.out=31)
      ys <- sapply(trypnts,f)
      dsy <- diff(sign(ys))
      if (any(dsy < 0)) {
        widx <- which(dsy < 0)
        intvl <- trypnts[widx + c(0,1)]
      }
    }
  uniroot(f=f,interval=intvl,extendInt='yes')$root
}

Testing on normal data

Here we test the code above on the problem considered in Theorem 5.2 of Lee et al. That is, we draw \(y \sim \mathcal{N}\left(\mu,\Sigma\right)\), then observe the value of \(F\) given in Theorem 5.2 when we plug in the actual population values of \(\mu\) and \(\Sigma\). This is several steps removed from our problem of inference on the SNR, but it is best to pause and make sure the implementation is correct first.

We perform 5000 simulations, letting \(p=20\), then creating a random \(\mu\) and \(\Sigma\), drawing a single \(y\), observing which element is the maximum, creating \(A, b, \nu\), then computing the \(F\) function, resulting in a \(p\)-value which should be uniform. We Q-Q plot those empirical \(p\)-values against a uniform law, finding them on the \(y=x\) line.

gram <- function(x) { t(x) %*% x }
rWish <- function(n,p=n,Sigma=diag(p)) { 
  require(mvtnorm)
  gram(rmvnorm(p,sigma=Sigma))
}
nsim <- 5000
p <- 20
A1 <- cbind(-1,diag(p-1))
set.seed(1234)
pvals <- replicate(nsim,{
  mu <- rnorm(p)
  Sigma <- rWish(n=2*p+5,p=p)
  y <- t(rmvnorm(1,mean=mu,sigma=Sigma) )
  # collect the maximum, so reorder the A above
  yord <- order(y,decreasing=TRUE)
  revo <- seq_len(p)
  revo[yord] <- revo

  A <- A1[,revo]
  nu <- rep(0,p)
  nu[yord[1]] <- 1
  b <- rep(0,p-1)
  foo <- ptn(y=y,A=A,b=b,nu=nu,mu=mu,Sigma=Sigma)
})
# plot them
library(dplyr)
library(ggplot2)
ph <- data_frame(pvals=pvals) %>%   
  ggplot(aes(sample=pvals)) + 
  geom_qq(distribution=stats::qunif) +
  geom_qq_line(distribution=stats::qunif) 
print(ph)

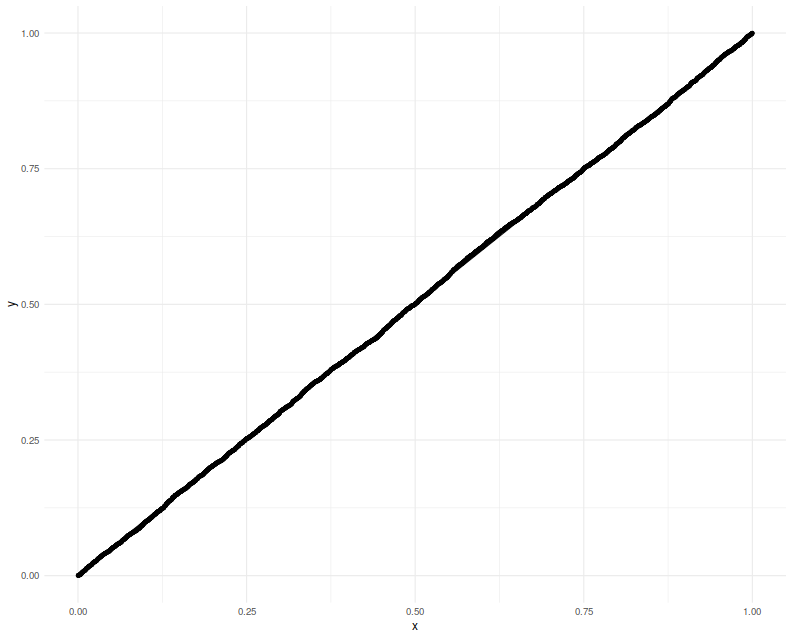
Now we attempt to use the confidence interval code. We construct a one-sided 95% confidence interval, and check how often it is violated by the \(\mu\) of the element which shows the highest \(y\). We will find that the empirical rate of violations of our confidence interval is indeed around 5%:

nsim <- 5000
p <- 20
A1 <- cbind(-1,diag(p-1))
set.seed(1234)
tgtval <- 0.95
viols <- replicate(nsim,{
  mu <- rnorm(p)
  Sigma <- rWish(n=2*p+5,p=p)
  y <- t(rmvnorm(1,mean=mu,sigma=Sigma) )
  # collect the maximum, so reorder the A above
  yord <- order(y,decreasing=TRUE)
  revo <- seq_len(p)
  revo[yord] <- revo

  A <- A1[,revo]
  nu <- rep(0,p)
  nu[yord[1]] <- 1
  b <- rep(0,p-1)
  # mu is unknown to this guy
  foo <- citn(p=tgtval,y=y,A=A,b=b,nu=nu,Sigma=Sigma)
  violated <- mu[yord[1]] < foo
})
print(sprintf('%.2f%%',100*mean(viols)))

## [1] "5.04%"

Testing on the Sharpe ratio

To use this machinery to perform inference on the SNR, we can either port the results to the multivariate \(t\)-distribution, which seems unlikely because uncorrelated marginals of a multivariate \(t\) are not independent. Instead we lean on the normal approximation to the vector of Sharpe ratios. If the \(p\)-vector \(x\) is normal with correlation matrix \(R\), then

where \(\hat{\zeta}\) is the \(p\)-vector of Sharpe ratios computed by observing \(n\) independent draws of \(x\), and \(\zeta\) is the \(p\)-vector of Signal Noise ratios. Note how this generalizes the 'Lo' form of the standard error of a scalar Sharpe ratio, viz \(\sqrt{(1 + \zeta^2/2)/n}\).

Here we will check the uniformity of \(p\) values resulting from using this normal approximation. This is closer to the actual inference we want to do, except we will cheat by using the actual \(R\) and \(\zeta\) to construct what is essentially the \(\Sigma\) to Lee's formulation. We will set \(p=20\) and draw 3 years of daily data. Again we plot the putative \(p\)-values against uniformity and find a good match.

# let's test it!
nsim <- 5000
p <- 20
ndays <- 3 * 252
A1 <- cbind(-1,diag(p-1))
set.seed(4321)

pvals <- replicate(nsim,{
  # population values here
  mu <- rnorm(p)
  Sigma <- rWish(n=2*p+5,p=p)
  RRR <- cov2cor(Sigma)
  zeta <- mu /sqrt(diag(Sigma))

  Xrets <- rmvnorm(ndays,mean=mu,sigma=Sigma) 
  srs <- colMeans(Xrets) / apply(Xrets,2,FUN=sd)

  y <- srs
  mymu <- zeta
  mySigma <- (1/ndays) * (RRR + (1/2) * diag(zeta) %*% (RRR * RRR) %*% diag(zeta))

  # collect the maximum, so reorder the A above
  yord <- order(y,decreasing=TRUE)
  revo <- seq_len(p)
  revo[yord] <- revo

  A <- A1[,revo]
  nu <- rep(0,p)
  nu[yord[1]] <- 1
  b <- rep(0,p-1)

  foo <- ptn(y=y,A=A,b=b,nu=nu,mu=mymu,Sigma=mySigma)
})
# plot them
library(dplyr)
library(ggplot2)
ph <- data_frame(pvals=pvals) %>%   
  ggplot(aes(sample=pvals)) + 
  geom_qq(distribution=stats::qunif) +
  geom_qq_line(distribution=stats::qunif) 
print(ph)

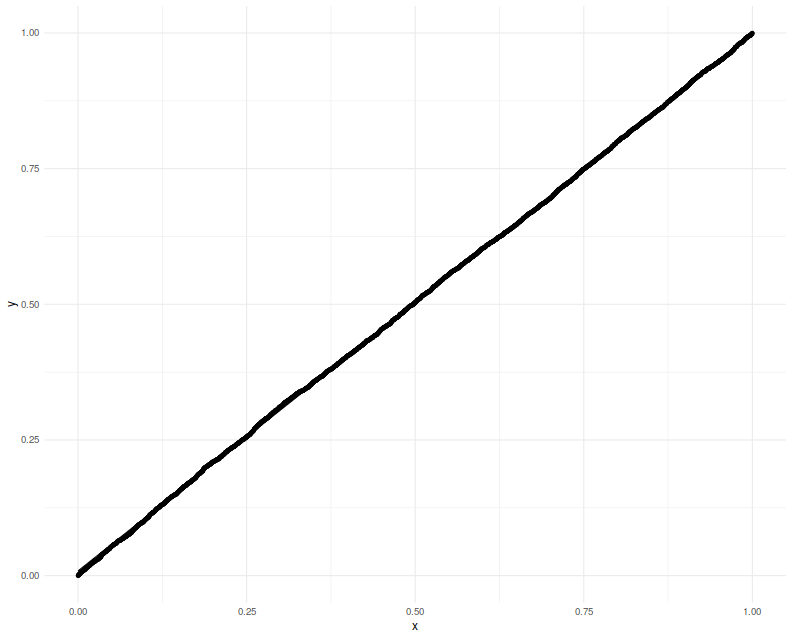
Lastly we make one more modification, filling in sample estimates for \(\zeta\) and \(R\) into the computation of the covariance. We compute one-sided 95% confidence intervals, and check how the empirical rate of violations. We find the rate to be around 5%.

nsim <- 5000
p <- 20
ndays <- 3 * 252
A1 <- cbind(-1,diag(p-1))
set.seed(9873)  # 5678 gives exactly 250 / 5000, which is eerie

tgtval <- 0.95
viols <- replicate(nsim,{
  # population values here
  mu <- rnorm(p)
  Sigma <- rWish(n=2*p+5,p=p)
  RRR <- cov2cor(Sigma)
  zeta <- mu /sqrt(diag(Sigma))

  Xrets <- rmvnorm(ndays,mean=mu,sigma=Sigma) 
  srs <- colMeans(Xrets) / apply(Xrets,2,FUN=sd)
  Sighat <- cov(Xrets)
  Rhat <- cov2cor(Sighat)

  y <- srs
  # now use the sample approximations. 
  # you can compute this from the observed information.
  mySigma <- (1/ndays) * (Rhat + (1/2) * diag(srs) %*% (Rhat * Rhat) %*% diag(srs))

  # collect the maximum, so reorder the A above
  yord <- order(y,decreasing=TRUE)
  revo <- seq_len(p)
  revo[yord] <- revo

  A <- A1[,revo]
  nu <- rep(0,p)
  nu[yord[1]] <- 1
  b <- rep(0,p-1)

  # mu is unknown to this guy
  foo <- citn(p=tgtval,y=y,A=A,b=b,nu=nu,Sigma=mySigma)
  violated <- zeta[yord[1]] < foo
})
print(sprintf('%.2f%%',100*mean(viols)))

## [1] "5.14%"

Putting it together

Lee's method appears to give nominal coverage for hypothesis tests and confidence intervals on the SNR of the asset with maximal Sharpe. In principle it should not be affected by correlation of the assets or by large differences in the SNRs of the assets. It should be applicable in the \(p > n\) case, as we are not inverting the covariance matrix. On the negative side, requiring one estimate the correlation of assets for the computation will not scale with large \(p\).

We are guardedly optimistic that this method is not adversely affected by the normal approximation of the Sharpe ratio, although it would be ill-advised to use it for the case of small samples until more study is performed. Moreover the quantile function we hacked together here should be improved for stability and accuracy.

Symmetric Confidence Intervals, and Choosing Sides

Consider the problem of computing confidence intervals on the Signal-Noise ratio, which is the population quantity \(\zeta = \mu/\sigma\), based on the observed Sharpe ratio \(\hat{\zeta} = \hat{\mu}/\hat{\sigma}\). If returns are Gaussian, one can compute 'exact' confidence intervals by inverting the CDF of the non-central \(t\) distribution with respect to its parameter. Typically instead one often uses an approximate standard error, using either the formula published by Johnson & Welch (and much later by Andrew Lo), or one using higher order moments given by Mertens, then constructs Wald-test confidence intervals.

Using standard errors yields symmetric intervals of the form

where \(s\) is the approximate standard error, and \(z_{\alpha/2}\) is the normal \(\alpha/2\) quantile. As typically constructed, the 'exact' confidence intervals based on the non-central \(t\) distributionare not symmetric in general, but are very close, and can be made symmetric. The symmetry condition can be expressed as

where \(c\) is some constant.

Picking sides

Usually I think of the Sharpe ratio as a tool to answer the question: Should I invest a predetermined amount of capital (long) in this asset? The Sharpe ratio can be used to construct confidence intervals on the Signal-Noise ratio to help answer that question.

Pretend instead that you are more opportunistic: instead of considering a predetermined side to the trade, you will observe historical returns of the asset. Then if the Sharpe ratio is positive, you will consider investing in the asset, and if the Sharpe is negative, you will consider shorting the asset. Can we rely on our standard confidence intervals now? After all, we are now trying to perform inference on \(\operatorname{sign}\left(\hat{\zeta}\right) \zeta\), which is not a population quantity. Rather it mixes up the population Signal-Noise ratio with information from the observed sample (the sign of the Sharpe). (Because of this mixing of a population quantity with information from the sample, real statisticians get a bit indignant when you try to call this a "confidence interval". So don't do that.)

It turns out that you can easily adapt the symmetric confidence intervals to this problem. Because you can multiply the inside of \(\left|\zeta - \hat{\zeta}\right|\) by \(\pm 1\) without affecting the absolute value, we have

Thus

are \(1-\alpha\) confidence intervals on \(\operatorname{sign}\left(\hat{\zeta}\right) \zeta\).

Although the type I error rate is maintained, the 'violations' of the confidence interval can be asymmetric. When the Signal Noise ratio is large (in absolute value), type I errors tend to occur on both sides of the confidence interval equally, because the Sharpe is usually the same sign as the Signal-Noise ratio. When the Signal-Noise ratio is near zero, however, typically the type I errors occur only on the lower side. (This must be the case when the Signal-Noise ratio is exactly zero.) Of course, since the Signal-Noise ratio is the unknown population parameter, you do not know which situation you are in, although you have some hints from the observed Sharpe ratio.

Before moving on, here we test the symmetric confidence intervals. We vary the Signal Noise ratio from 0 to 2.5 in 'annual units', draw two years of daily normal returns with that Signal-Noise ratio, pick a side of the trade based on the sign of the Sharpe ratio, then build symmetric confidence intervals using the standard error estimator \(\sqrt{(1 + \hat{\zeta}^2/2)/n}\). We build the 95% confidence intervals, then note any breaches of the upper and lower confidence bounds. We repeat this 10000 times for each choice of SNR.

We then plot the type I rate for the lower bound of the CI, the upper bound and the total type I rate, versus the Signal Noise ratio. We see that the total empirical type I rate is very near the nominal rate of 5%, and this is entirely attributable to violations of the lower bound up until a Signal Noise ratio of around 1.4 per square root year. At around 2.5 per square root year, the type I errors are observed in equal proportion on both sides of the CI.

suppressMessages({
  library(dplyr)
  library(tidyr)
  # https://cran.r-project.org/web/packages/doFuture/vignettes/doFuture.html
  library(doFuture)
  registerDoFuture()
  plan(multiprocess)
})
# run one simulation of normal returns and CI violations
onesim <- function(n,pzeta,zalpha=qnorm(0.025)) {
    x <- rnorm(n,mean=pzeta,sd=1)
    sr <- mean(x) / sd(x)
    se <- sqrt((1+0.5*sr^2)/n)
    cis <- abs(sr) + se * abs(zalpha) * c(-1,1)
    pquant <- sign(sr) * pzeta
    violations <- c(pquant < cis[1],pquant > cis[2])
}
# do a bunch of sims, then sum the violations of low and high;
repsim <- function(nrep,n,pzeta,zalpha) {
  jumble <- replicate(nrep,onesim(n=n,pzeta=pzeta,zalpha=zalpha))
  retv <- t(jumble)
  colnames(retv) <- c('nlo','nhi')
  retv <- as.data.frame(retv) %>%
        summarize_all(.funs=sum)
    retv$nrep <- nrep
    invisible(retv)
}
manysim <- function(nrep,n,pzeta,zalpha,nnodes=7) {
  if (nrep > 2*nnodes) {
    # do in parallel.
    nper <- table(1 + ((0:(nrep-1) %% nnodes))) 
    retv <- foreach(i=1:nnodes,.export = c('n','pzeta','zalpha','onesim','repsim')) %dopar% {
      repsim(nrep=nper[i],n=n,pzeta=pzeta,zalpha=zalpha)
    } %>%
      bind_rows() %>%
            summarize_all(.funs=sum) 
  } else {
    retv <- repsim(nrep=nrep,n=n,pzeta=pzeta,zalpha=zalpha)
  }
    # turn sums into means
    retv %>%
        mutate(vlo=nlo/nrep,vhi=nhi/nrep) %>%
        dplyr::select(vlo,vhi)
}

# run a bunch
ope <- 252
nyr <- 2
alpha <- 0.05

# simulation params
params <- data_frame(zetayr=seq(0,2.5,by=0.0625)) %>%
    mutate(pzeta=zetayr/sqrt(ope)) %>%
    mutate(n=round(ope*nyr))

# run a bunch
nrep <- 100000
set.seed(4321)
system.time({
results <- params %>%
  group_by(zetayr,pzeta,n) %>%
    summarize(sims=list(manysim(nrep=nrep,nnodes=7,
                                pzeta=pzeta,n=n,zalpha=qnorm(alpha/2)))) %>%
  ungroup() %>%
  tidyr::unnest() 
})

suppressMessages({
  library(dplyr)
  library(tidyr)
  library(ggplot2)
})
ph <- results %>%
    mutate(vtot=vlo+vhi) %>%
    gather(key=series,value=violations,vlo,vhi,vtot) %>%
    mutate(series=case_when(.$series=='vlo' ~ 'below lower CI',
                                                    .$series=='vhi' ~ 'above upper CI',
                                                    .$series=='vtot' ~ 'outside CI',
                                                    TRUE ~ 'error')) %>%
    ggplot(aes(zetayr, violations, colour=series)) + 
    geom_line() + geom_point(alpha=0.5) + 
    geom_hline(yintercept=c(alpha/2,alpha),linetype=2,alpha=0.5) +
    labs(x='SNR (per square root year)',y='type I rate',
             color='error type',title='rates of type I error when trade side is sign of Sharpe')
print(ph)

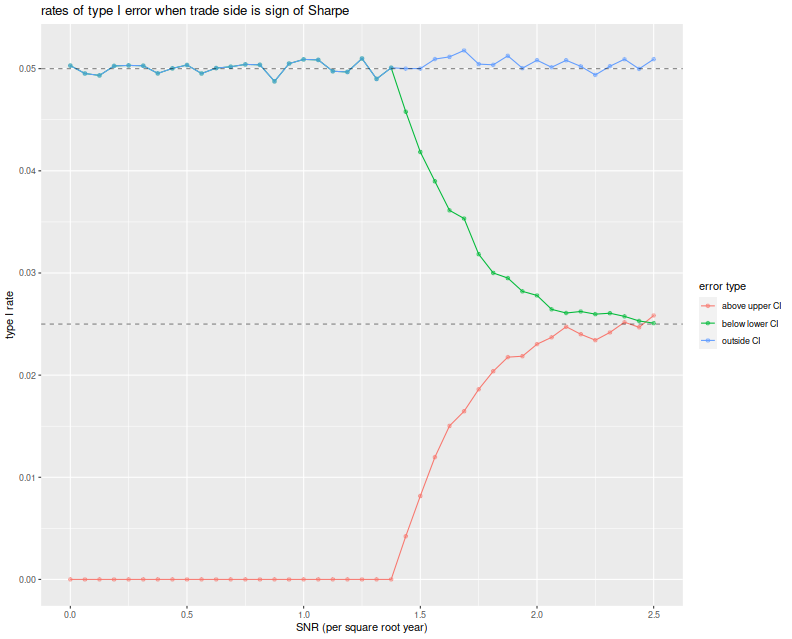
A Bayesian Donut?

Of course, this strategy seems a bit unrealistic: what's the point of constructing confidence intervals if you are going to trade the asset no matter what the evidence? Instead, consider a fund manager whose trading strategies are all above average: she/he observes the Sharpe ratio of a backtest, then only trades a strategy if \(|\hat{\zeta}| \ge c\) for some sufficiently large \(c\), and picks a side based on \(\operatorname{sign}\left(\hat{\zeta}\right)\). This is a 'donut'.

Conditional on observing \(|\hat{\zeta}| \ge c\), can one construct a reliable confidence interval on \(\operatorname{sign}\left(\hat{\zeta}\right) \zeta\)? Perhaps our fund manager thinks there is no point in doing so if \(c\) is sufficiently large. I think to do so you have to make some assumptions about the distribution of \(\zeta\) and rely on Baye's law. We did not say what would happen if the junior quant at this shop developed a strategy where \(|\hat{\zeta}| < c\), but presumably the junior quants were told to keep working until they beat the magic threshold. If the junior quants only produce strategies with small \(\zeta\), one suspects that the \(c\) threshold does very little to reject bad strategies, rather it just slows down their deployment. (In response the quants will surely beef up their backtesting infrastructure, or invent automatic strategy generation.)

Generalizing to higher dimensions

The real interesting question is what this looks like in higher dimensions. Now one observes \(p\) assets, and is to construct a portfolio on those assets. Can we construct good confidence intervals on the Sharpe ratio of the chosen portfolio? In this setting we have many more possible choices, so a general purpose analysis seems unlikely. However, if we restrict ourselves to the Markowitz portfolio, I suspect some progress can be made. (Although I have been very slow to make it!) I hope to purse this in a followup blog post.